在数学的浩瀚宇宙中，排列与组合作为离散数学的重要分支，不仅揭示了事物间错综复杂的关系，还蕴含着深刻的逻辑美与秩序感，我们将聚焦于一个具体的排列——35412，探讨其逆序数的奥秘，一窥数学世界的精妙与趣味。

逆序数定义初探

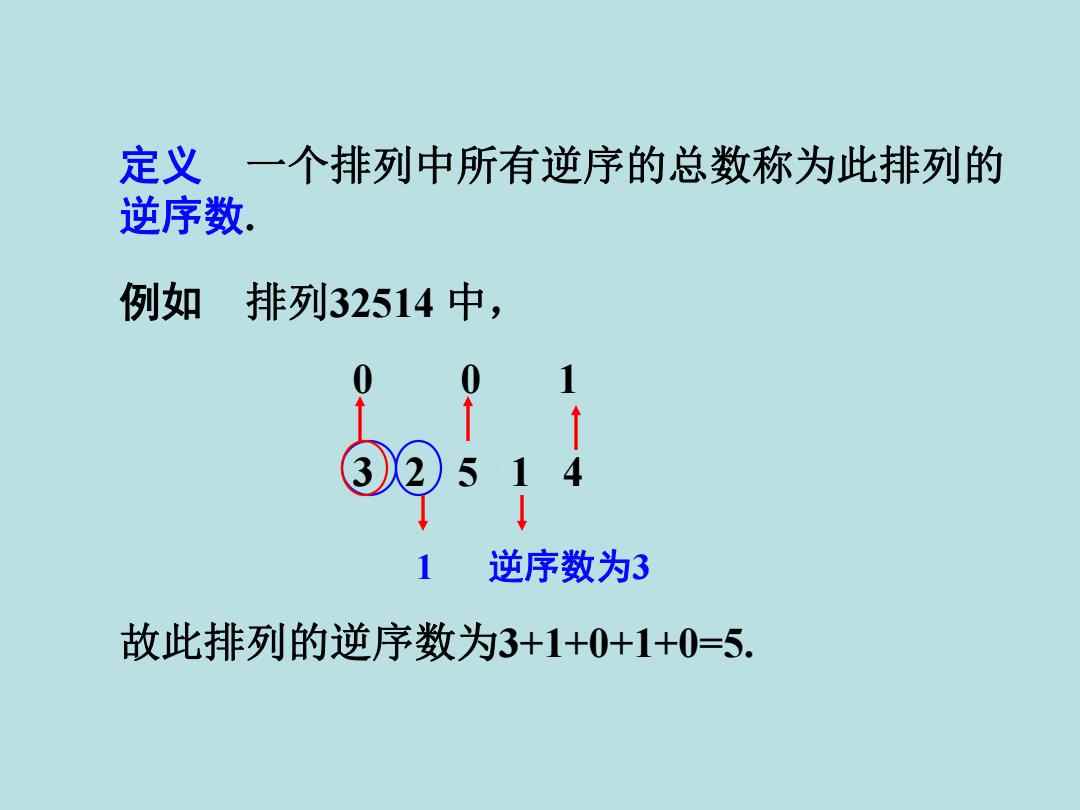
逆序数，又称为逆序对的数量，是衡量一个排列中元素间相对顺序不协调程度的量度，具体而言，对于一个排列p1, p2, ..., pn，如果pi > pj 且i < j（即较小的数位于较大的数之后），则称(i, j) 是一个逆序对，一个排列的逆序数即为该排列中所有逆序对的总数。

排列35412的逆序数计算

我们来计算排列35412的逆序数，我们逐一检查每个元素与其后元素的关系：

- 对于数字3，它位于第一位，没有后续元素与之形成逆序对，故不计入逆序数。

- 对于数字5，它在第二位，由于5>3（且3在5之前），不构成逆序对；但需考虑其后数字4和2，其中5>4且4在5之前，形成一对逆序对；同样地，5>2且2在5之前，又形成一对逆序对，对于数字5，共贡献2个逆序对。

- 数字4在第三位，它大于前面的3但小于后面的5和2，因此不增加新的逆序对。

- 数字1在第四位，它小于其后的数字2，形成一对逆序对（1<2且2在1之后）。

- 数字2在第五位，它小于前面的所有数字（但这些已在之前计算过），故不增加新的逆序对。

排列35412的逆序数为：0（来自3）+ 2（来自5）+ 0（来自4）+ 1（来自1）+ 0（来自2）= 3，排列35412的逆序数是3。

逆序数的性质与意义

逆序数不仅是排列理论中的一个基本概念，还具有广泛的应用价值：

1、在统计学中的应用：在分析数据排序、概率分布等问题时，逆序数可以帮助我们理解数据间的相对位置关系，进而推断出某些统计特性。

2、算法设计：在计算机科学中，逆序数的概念常用于优化算法设计，如快速排序、归并排序等算法的效率分析中，通过减少逆序数，可以提升数据处理的效率。

3、数学问题求解：在解决一些组合数学问题时，如计算特定排列的个数、判断一个排列是否为最长递增子序列等，逆序数是一个重要的辅助工具。

4、数学美学的体现：逆序数的概念体现了数学中的对称美与和谐美，通过计算和比较不同排列的逆序数，我们可以发现其中蕴含的规律和模式，这不仅是数学逻辑的体现，也是对自然界和人类社会秩序的一种抽象理解。

排列35412的逆序数计算方法拓展

除了上述逐一检查的方法外，还可以利用更高效的算法来计算任意排列的逆序数：

归并排序思想：利用归并排序的思想，将原始序列不断二分直到成为单个元素，然后自底向上合并时计算每个子序列的逆序对总数，这种方法的时间复杂度为O(n log n)，比直接逐一检查的方法更为高效。

树状数组（Fenwick Tree）：树状数组是一种数据结构，可以高效地解决一系列关于前缀和、排名、逆序对数量等问题，通过构建树状数组并利用其特性，可以快速计算出给定排列的逆序数，这种方法同样具有O(n log n)的时间复杂度。

离线算法与在线算法：对于某些特定问题（如静态数据集），我们可以采用离线算法预先计算所有可能的逆序对；而对于需要实时处理的数据流（如在线排序），则需设计在线算法以较低的时间复杂度进行动态更新和查询。

通过对排列35412的逆序数的探究，我们不仅加深了对这一数学概念的理解，还领略了数学在解决实际问题中的灵活应用，从逐一检查到利用高级数据结构优化计算过程，每一种方法都展现了人类智慧在探索未知过程中的不懈努力，正如排列组合的魅力所在——它们不仅仅是冰冷的公式和定理，更是连接现实世界与抽象思维的桥梁，激发着我们对未知世界的好奇与探索欲，在未来的学习与研究中，让我们继续以数学的眼光观察世界，以逻辑的力量破解难题，共同揭开更多隐藏于日常生活中的数学奥秘。